CCH'S BLOG

sha256 哈希算法分析

2023/02/28 algorithm 共 4194 字，约 12 分钟

概述

SHA256属于著名的SHA家族⼀员。SHA（Secure Hash Algorithm，安全哈希算法）是⼀类由美国国家标准与技术研究院 （NIST）发布的密码哈希函数。正式名称为SHA的第⼀个成员发布于 1993年，两年之后，著名的SHA-1发布，之后另外的多种变体相继发布，包括SHA224、SHA256、SHA384、SHA512、SHA-512/224和SHA-512/256，这些变体除了生成摘要的长度、循环运行的次数等一些细微差异之外，基本结构是一致的，这些算法也被称作SHA2。SHA256算法是SHA2算法簇中的⼀类。对于任意长度的消息，SHA256会产⽣⼀个256位的消息摘要。SHA256具有密码哈希函数的⼀般特性。

以空字符串为例，几种不同的哈希算法生成的结果如下

SHA224("")
0x d14a028c2a3a2bc9476102bb288234c415a2b01f828ea62ac5b3e42f
SHA256("")
0x e3b0c44298fc1c149afbf4c8996fb92427ae41e4649b934ca495991b7852b855
SHA384("")
0x 38b060a751ac96384cd9327eb1b1e36a21fdb71114be07434c0cc7bf63f6e1da274edebfe76f65fbd51ad2f14898b95b
SHA512("")
0x cf83e1357eefb8bdf1542850d66d8007d620e4050b5715dc83f4a921d36ce9ce47d0d13c5d85f2b0ff8318d2877eec2f63b931bd47417a81a538327af927da3e
SHA512/224("")
0x 6ed0dd02806fa89e25de060c19d3ac86cabb87d6a0ddd05c333b84f4
SHA512/256("")
0x c672b8d1ef56ed28ab87c3622c5114069bdd3ad7b8f9737498d0c01ecef0967a

算法可视化工具

sha256 算法可视化

参考

wiki

一文读懂SHA256算法原理及其实现

SHA256算法原理详解

sha256 原理

对于任意长度的消息，SHA256都会产生一个256位的哈希值，称作消息摘要。如 hello 经过 sha256 哈希函数后转化为 2cf24dba5fb0a30e26e83b2ac5b9e29e1b161e5c1fa7425e73043362938b9824，下面我们就来分析 hello 的转化过程。

常量初始化

sha256 算法的计算过程中用到了8个哈希初值和64个哈希常量。

其中，由自然数中前8个质数(2,3,5,7,11,13,17,19)的平方根的小数部分取前32bit的8个哈希初值如下

a := 01101010000010011110011001100111 0x6a09e667
b := 10111011011001111010111010000101 0xbb67ae85
c := 00111100011011101111001101110010 0x3c6ef372
d := 10100101010011111111010100111010 0xa54ff53a
e := 01010001000011100101001001111111 0x510e527f
f := 10011011000001010110100010001100 0x9b05688c
g := 00011111100000111101100110101011 0x1f83d9ab
h := 01011011111000001100110100011001 0x5be0cd19

tips:

\[\sqrt{2} = 1.414213562373095048\]

将 1.414213562373095048 转化为二进制为 **0**01111111111**0110101000001001111001100110011111110011101111001101**取小数部分的前32位 0110 1010 0000 1001 1110 0110 0110 0111即对应16进制 6a09e667

由自然数中前64个质数(2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97…)的立方根的小数部分取前32bit的64个哈希初值如下

0x428a2f98, 0x71374491, 0xb5c0fbcf, 0xe9b5dba5, 0x3956c25b, 0x59f111f1, 0x923f82a4, 0xab1c5ed5,
0xd807aa98, 0x12835b01, 0x243185be, 0x550c7dc3, 0x72be5d74, 0x80deb1fe, 0x9bdc06a7, 0xc19bf174,
0xe49b69c1, 0xefbe4786, 0x0fc19dc6, 0x240ca1cc, 0x2de92c6f, 0x4a7484aa, 0x5cb0a9dc, 0x76f988da,
0x983e5152, 0xa831c66d, 0xb00327c8, 0xbf597fc7, 0xc6e00bf3, 0xd5a79147, 0x06ca6351, 0x14292967,
0x27b70a85, 0x2e1b2138, 0x4d2c6dfc, 0x53380d13, 0x650a7354, 0x766a0abb, 0x81c2c92e, 0x92722c85,
0xa2bfe8a1, 0xa81a664b, 0xc24b8b70, 0xc76c51a3, 0xd192e819, 0xd6990624, 0xf40e3585, 0x106aa070,
0x19a4c116, 0x1e376c08, 0x2748774c, 0x34b0bcb5, 0x391c0cb3, 0x4ed8aa4a, 0x5b9cca4f, 0x682e6ff3,
0x748f82ee, 0x78a5636f, 0x84c87814, 0x8cc70208, 0x90befffa, 0xa4506ceb, 0xbef9a3f7, 0xc67178f2

信息预处理

以字符串 hello 为例 1、首先将字符串转化为UTF8编码的二进制并在结尾补位一个bit为1，如 hello转化为二进制为 01101000 01100101 01101100 01101100 01101111,并在内容结尾添加一个为1的bit。 2、整个预处理后的块的bit位数要满足512的整数倍，并在一整块的最后64位添加原始消息的长度。如这里的 hello 比特位数位40，则在最后64位以大端模式存放 101000。 3、在块中的消息体和最后64位长度之间补位0bit，使整个块的大小满足`消息体大小 + 1个1bit补位 + N个0bit补位 + 64bit长度 = 512的整数倍。

hello 的预处理块内容如下：

Message block - 512 Bits
01101000 01100101 01101100 01101100
01101111 10000000 00000000 00000000
00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000
00000000 00000000 00000000 00101000

逻辑处理

sha256_logic

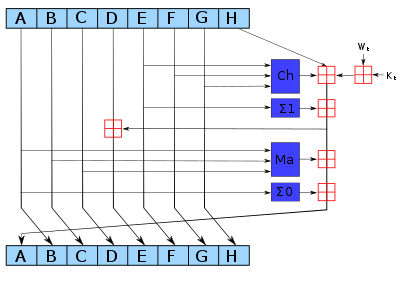
SHA-2 系列压缩函数中的一次迭代。蓝色组件执行以下操作

\[\begin{array}{l} \mathrm{Ch}(E, F, G)=(E \wedge F) \oplus(\neg E \wedge G) \\ \mathrm{Ma}(A, B, C)=(A \wedge B) \oplus(A \wedge C) \oplus(B \wedge C) \\ \Sigma_{0}(A)=(A \gg 2) \oplus(A \gg 13) \oplus(A \gg 22) \\ \Sigma_{1}(E)=(E \gg 6) \oplus(E \gg 11) \oplus(E \gg 25) \end{array}\]

σ0 = (x S^n 7) ⊕ (x S^n 18) ⊕ (x R^n 3)

σ1 = (x S^n 17) ⊕ (x S^n 19) ⊕ (x R^n 10)

SHA-512 按位循环使用不同的常量。红色 ⊞ 是 SHA-256 的加法模 2^32，SHA-512 则是加法模 2^64。

tips:

逻辑运算含义
∧按位“与”
¬按位“补”
⊕按位“异或”
S^n循环右移n个bit
R^n右移n个bit

计算消息摘要

将消息体按512bit分成多个块

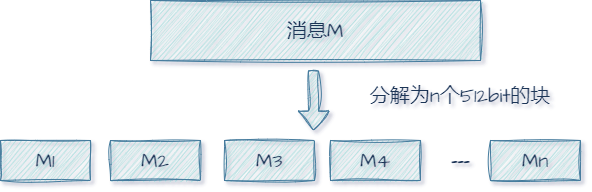
每个块对应64字的大块，一个字32bit

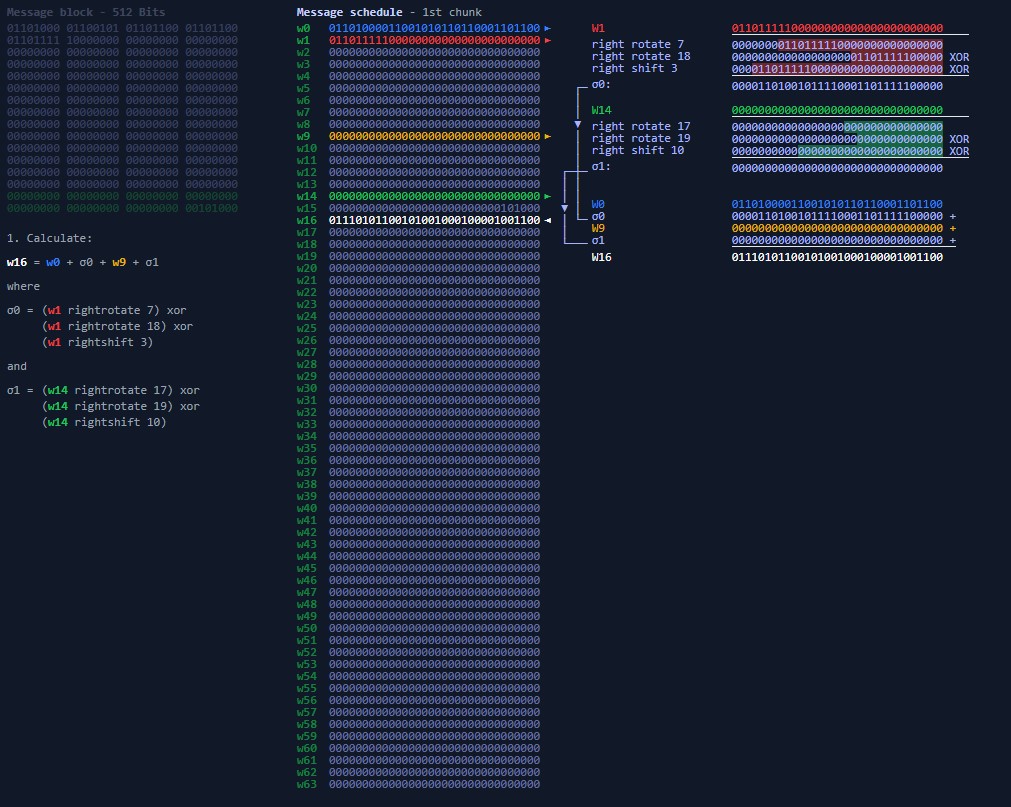
如上图所示

w16 由前面的字经过移位变换运算得出，以此类推，一直循环算出w63的值

计算此块的消息摘要 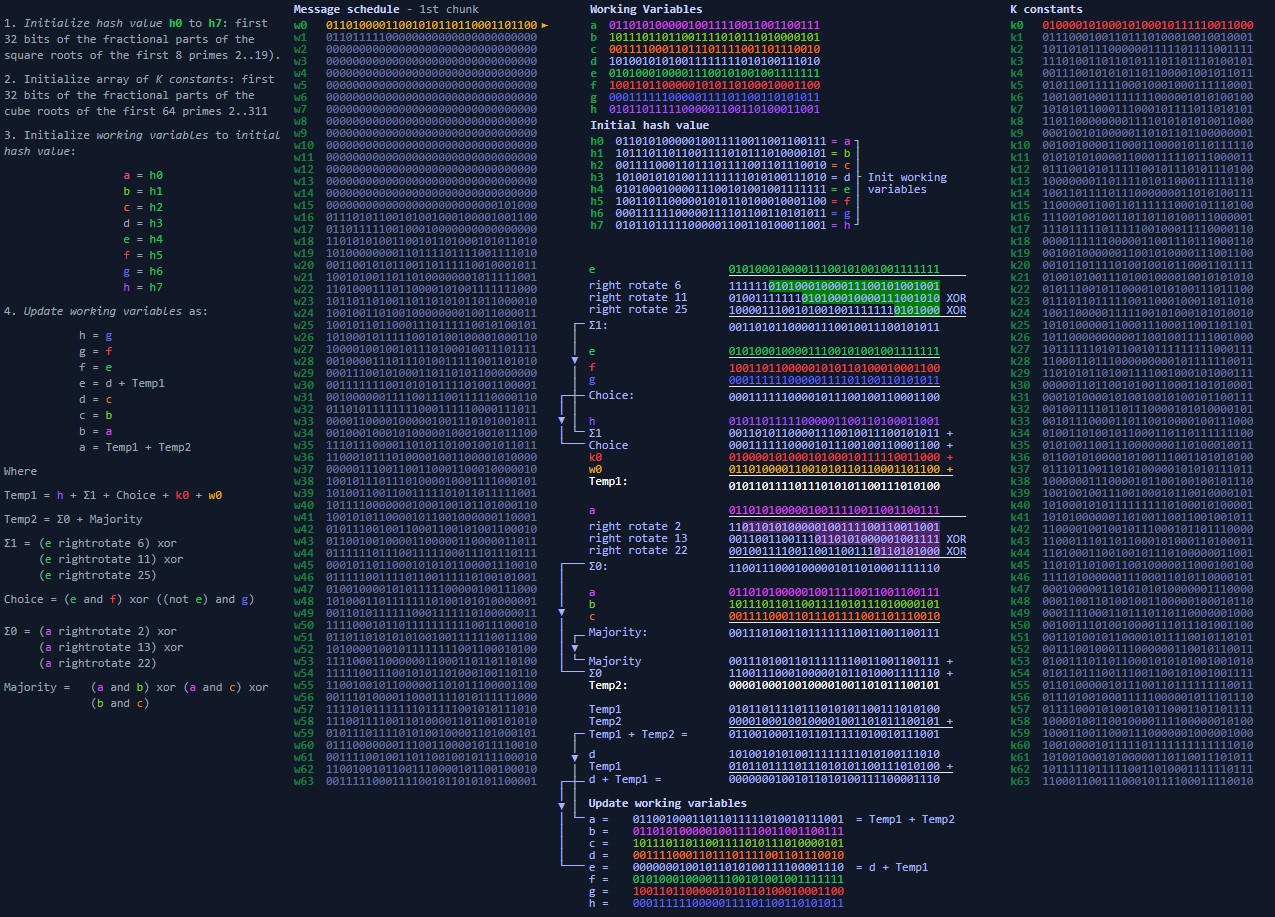如上图所示，a~h和h0~h7的初值为之前算出前8个质数的平方根的32小数部分，k0~k63为之前算出前64个质数的立方根的32小数部分。根据w0~w63和k0~k63的值经过移位变换运算不断迭代a~h的值，如消息体只有512bit,则sha256的结果值为

h0 = h0 + a
h1 = h1 + b
h2 = h2 + c
h3 = h3 + d
h4 = h4 + e
h5 = h5 + f
h6 = h6 + g
h7 = h7 + h

Sha256 = h0 h1 h2 h3 h4 h5 h6 h7

如消息体有多个512bit的块，则前一个块算出h0~h7的值带入下一个块的a~h和h0~h7的初值，以此类推直到算出最后一个块的h0~h7

文档信息

Search

    Table of Contents